Asymptotes these are lines for which the graph is undefined (this means that the curve does not cross asymptotes) Remember that you cannot divide by zero Therefore, in the graph of 1/(1 x), x = 1 is an asymptote because when x is 1, you end up dividing by zero A curve often gets very close to an asymptote, without actually crossing itShort‐run aggregate supply curveThe short‐run aggregate supply (SAS) curve is considered a valid description of the supply schedule of the economy only in the short‐run The short‐run is the period that begins immediately after an increase in the price level and that ends when input prices have increased in the same proportion to the increase in the price levelNoise Rating NR is commonly used in Europe

Two Examples Of Eustatic Sea Level Curves That Show Significant Download Scientific Diagram
Level curves examples
Level curves examples-Set title "Sometimes it helps to use multiplot" set view map set xr 0515 set yr 015 unset xlabel unset ylabel set tics scale 00 set lmargin at screen 01 set rmargin at screen 09 set bmargin at screen 01 set tmargin at screen 09 set multiplot set cntrparam levels discrete 01, 10, 100, 1000 set isosamples 500,100 splot Rosenbrock(x,y) with lines lc rgb "#" set isosamples · Here is the parametric curve for this example Notice that with this sketch we started and stopped the sketch right on the points originating from the end points of the range of \(t\)'s Contrast this with the sketch in the previous example where we had a portion of the sketch to the right of the "start" and "end" points that we computed



Level Curves Examples Done In Mathematica Last Modified Spring 14
I am not sure how to apply level curves or contour lines for complex Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn,Level curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −y The set x2 − y2 = 1 consists of two hyperbola with with their "noses" at the point (−1,0) and (1,0) The set x2 − y2 = −1 consists of two hyperbola with their noses at (0,1) and (0,−1) Drawing several contour curves {f(x,y) = c }It looks much like a topographic map of the surface In figure 1412 both the surface and its associated level curves are shown Note that, as with a topographic map, the heights corresponding to the level curves are evenly spaced, so that where curves are closer
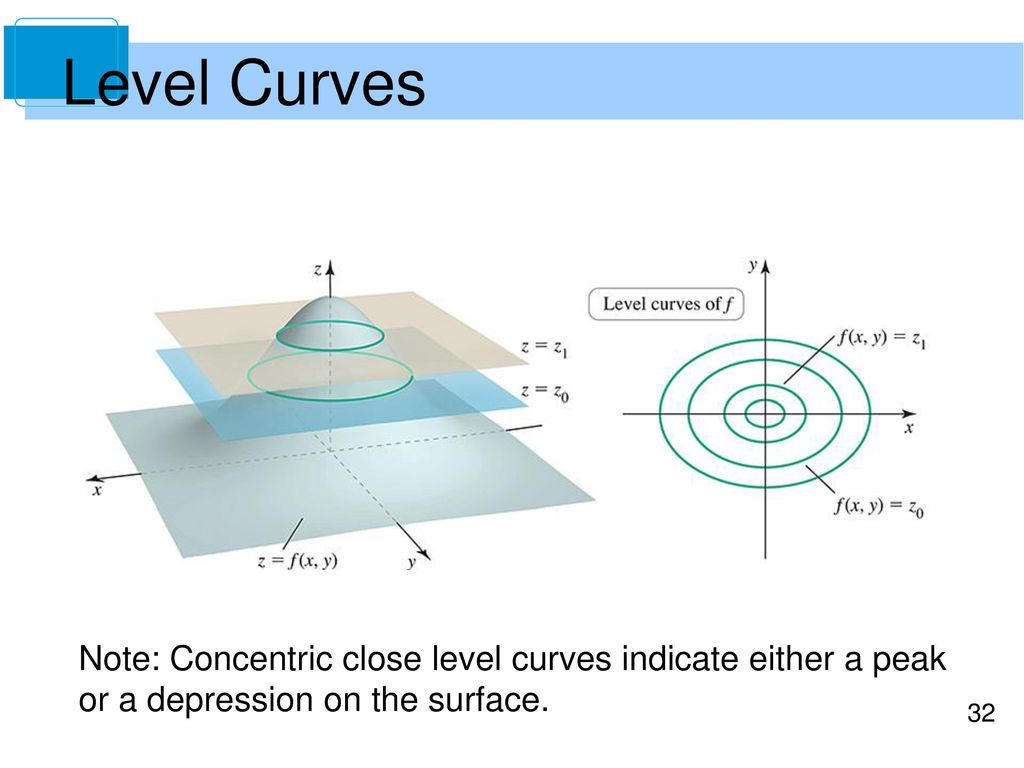
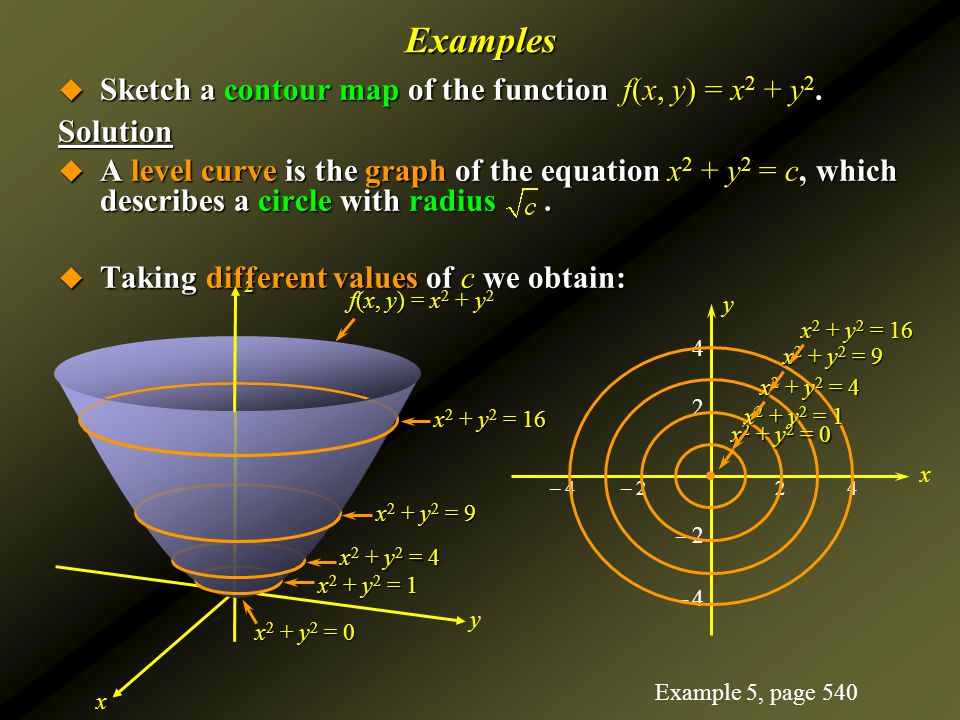
One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation Notice that if you walk along one of these contour lines you neither ascend nor descend Figure · A level curve of a function f (x,y) is a set of points (x,y) in the plane such that f (x,y)=c for a fixed value c Example 5 The level curves of f (x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of cCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean
Level Curves and Level Surfaces Line Integrals Optimization and Related Rates Optimization for Functions of 2 Variables Parametric Equations 2space Parametric Equations 3space Partial Derivatives Polar Coordinate System Polar Coordinates Derivatives and Integrals PreCalculus Riemann Sums and the Fundamental Theorem of Calculus 2dIn this Photo Editing tutorial, we'll look at the similarities between two of Photoshop's most important image editing tools the Levels and Curves adjustments At first glance, the Curves adjustment may seem less like an image editing tool and more like something only a scientist would know what to do with, especially when compared with the much simpler Levels adjustment whichPage 9 of 15 NSPS CST Level III Sample Examination Survey Computations 22 The notes for a threewire level run from BM A TO BM B are shown for the two setups required If elevation of BM A is 3187, compute the elevation of BM B a 3733, 2657, 1580 b 46, 34, 2750 c 2247, 1185, 0124 d



Level Set Wikipedia



How To Sketch Level Curves Youtube
· For example, all possible combinations of hamburgers or movies that report to the person the same level of utility or satisfaction The indifference curve simply reflects the preferences between pairs of goods and has no relation to money or pricesA graph of some level curves can give a good idea of the shape of the surface;More Lessons for ALevel Maths Math Worksheets Examples, solutions, videos, activities and worksheets that are suitable for A Level Maths How to find the area bounded by a curve above the xaxis (tutorial 1) Find the area bounded by the curve y = x 2 1, the lines x =


Making Difficulty Curves In Games Stuff Made By Dave



Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram
· The Levels Dialog Both Levels and Curves display a histogram of your image to help inform the adjustments you make In the Levels dialog, you'll see a couple of sliders The first is the input levels As you move the shadows slider from the left to the right, everything to the left of the slider will turn to pure blackA level curve or a conservation law is an equation of the form U(x;y) = c Hikers like to think of Uas the altitude at position (x;y) on the map and U(x;y) = cas the curve which represents the easiest walking path, that is, altitude does not change along that route The altitude is conserved along the route, hence the terminology conservation law Other examples of level curves are isobars andColorFunction is supplied with a single argument, given by default by the average of the scaled values of f for each pair of successive contour levels With the default settings Exclusions > Automatic and ExclusionsStyle > None , ContourPlot breaks continuity in its sampling at any discontinuity curve it detects



Level Sets Ximera


Section 13 1 Level Curves Youtube
· Indifference curve shows various combinations are so, arranged in order to show different levels of satisfaction, each level of satisfaction being marked in ordinal numbers as first, second, or third Now properties of indifference curve with diagram are definesThe result can be finetuned with the R, G, and B curves like in the previous example The curve for C is used to compensate for the increased contrast that is a side effect of setting Black and White LevelsAs an example, the same level of output could be achieved by a company when capital inputs increase, but labor inputs decrease Property 2 An isoquant curve



Introduction To Functions Of Several Variables Ppt Download



Solved Multivariable Functions And Level Curvesi M Having Chegg Com
The level curves of $f(x,y)$ are curves in the $xy$plane along which $f$ has a constant value The level surfaces of $f(x,y,z)$ are surfaces in $xyz$space on which $f$ has a constant value Sometimes, level curves or surfaces are referred to as level setsLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1 On the graphThere is a Maple command that will plot several level curves in the same plot for a given function with evenly spaced values of c For example, to plot level curves for the above function f (x,y), use the command > contourplot (x^2y^2,x=22,y=22,scaling=constrained,



Level Curves Examples



Solved In Calculus I And Ii We Worked With Functions Dep Chegg Com
Worked example 72 Circular Up Circular motion Previous Motion on curved surfaces Worked example 71 A banked curve Question Civil engineers generally bank curves on roads in such a manner that a car going around the curve at the recommended speed does not have to rely on friction between its tires and the road surface in order to round the curve Suppose that theFor example, the xaxis may measure the quantity of food available while the yaxis measures the risk involved in obtaining it The indifference curve is drawn to predict the animal's behavior at various levels of risk and food availability Criticisms Indifference curves inherit the criticisms directed at utility more generallyLevel curves, or contours, are the curves corresponding to the equation f(x,y)=h for various fixed values of the elevation z=h For example on a topopmap they might be traced for every etc) Often a thicker line is used for every



Level Curves Examples Done In Mathematica Last Modified Spring 14


Matplotlib Contour Plot Tutorialspoint
Level Curves give me the function f (x,y) Give me a value of Z 4 3 2 1 0 1 2 3 4 Give me another function f (f,y) Give me another value of Z 4 3 2 1 0 1 2 3 4For example, if c = − 1, the level curve is the graph of x 2 2 y 2 = 1 In the level curve plot of f (x, y) shown below, the smallest ellipse in the center is when c = − 1 Working outward, the level curves are for c = − 2, − 3, , − 10 · Of course, we probably don't have the function that gives the elevation, but we can at least graph the contour curves Let's do a quick example of this Example 3 Identify the level curves of f (x,y) = √x2 y2 f (x, y) = x 2 y 2 Sketch a few of them



Solved 3 Points Writing Prompt 1 Typed 100 0 Words Chegg Com


Introduction To Functions Of Several Variables Ppt Download
The noise rating graphs for different sound pressure levels are plotted at acceptable sound pressure levels at different frequencies Acceptable sound pressure level vary with the room and the use of it Different curves are obtained for each type of use Each curve is obtained by a NR number Note!Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour ofMath 3 Level Curves Examples Prof Yuen (Match level curves with surfaces) (A) (B) (D)



How To Find The Level Curves Of A Function Calculus 3 Youtube


Hypsometric Curve
Here is an example to understand the indifference curve better Peter has 1 unit of food and 12 units of clothing Now, we ask Peter how many units of clothing is he willing to give up in exchange for an additional unit of food so that his level of satisfaction remains unchangedExample The level curve is at the level k = 1 2 32 = 10, or x y2 = 10 (Notice that we have guaranteed that the point is on this level curve) Now consider the gradient vector at the point (a;b), which we denote byAnother example is the two variable realvalued function $f(x, y) = x^2 y^2$ which represents a hyperboloid The level curves generated by the planes $z = 1$, $z = 2$, and $z = 3$ are hyperbolas The image below depicts the level curve of this hyperboloid corresponding to $z = 1$


8 Calculus Of Several Variables Functions Of Several Variables Ppt Download



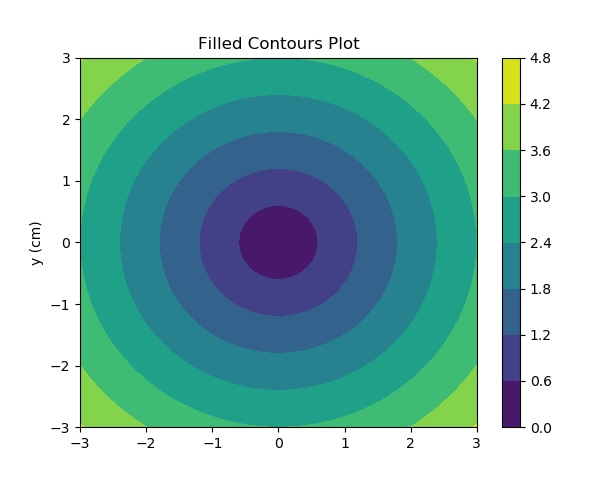
Plotting Using Contour In Python Epythonguru
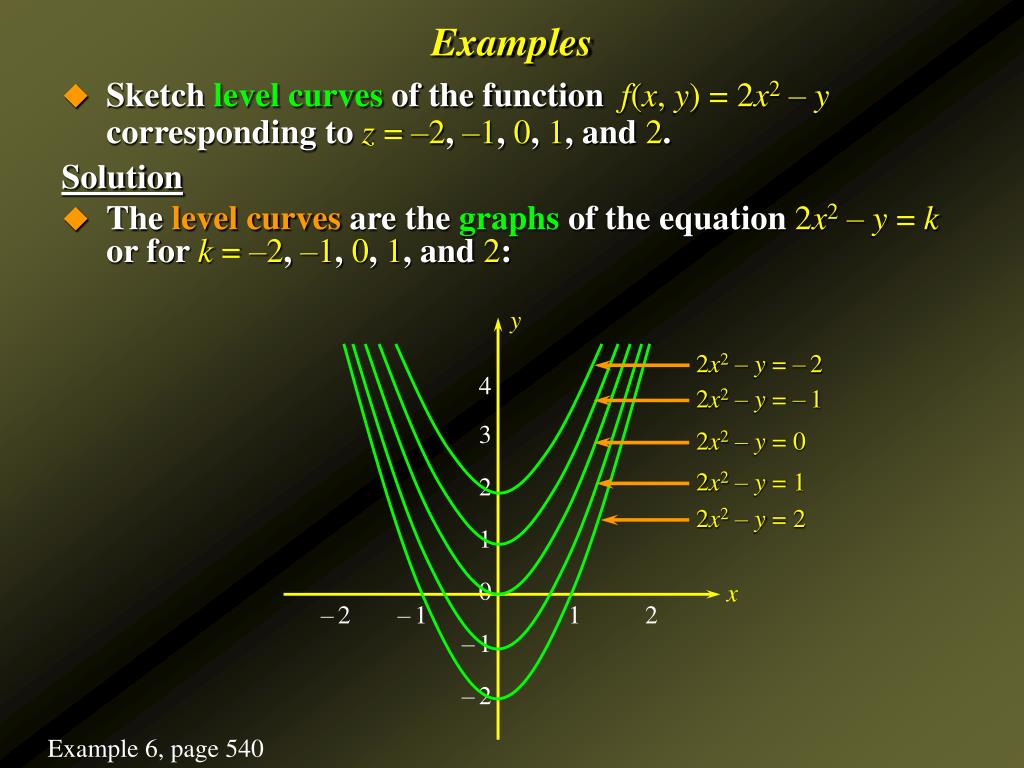
Level curves are 2 variable functions of x and y, which produce different levels of curve for their values (123,n), for example, x^2y^=c, for different values of x and y, (1,2,3,) will give different levels of circlesFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andExample 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c



Level Curves



Level Set Examples Math Insight
For example, "largest * in the world" Search within a range of numbers Put between two numbers For example, camera $50$100Example 1 (Solution Strategy) Sketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map · Grading on a curve is a term that describes a variety of different methods that a teacher uses to adjust the scores her students received on a test in some way Most of the time, grading on a curve boosts the students' grades by moving their actual scores up a few notches, perhaps increasing the letter gradeSome teachers use curves to adjust the scores received in



Level Curves In Mathbb R 3 Mathematics Stack Exchange


Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id


Extra Explanation Wiskunde Op Tilburg University



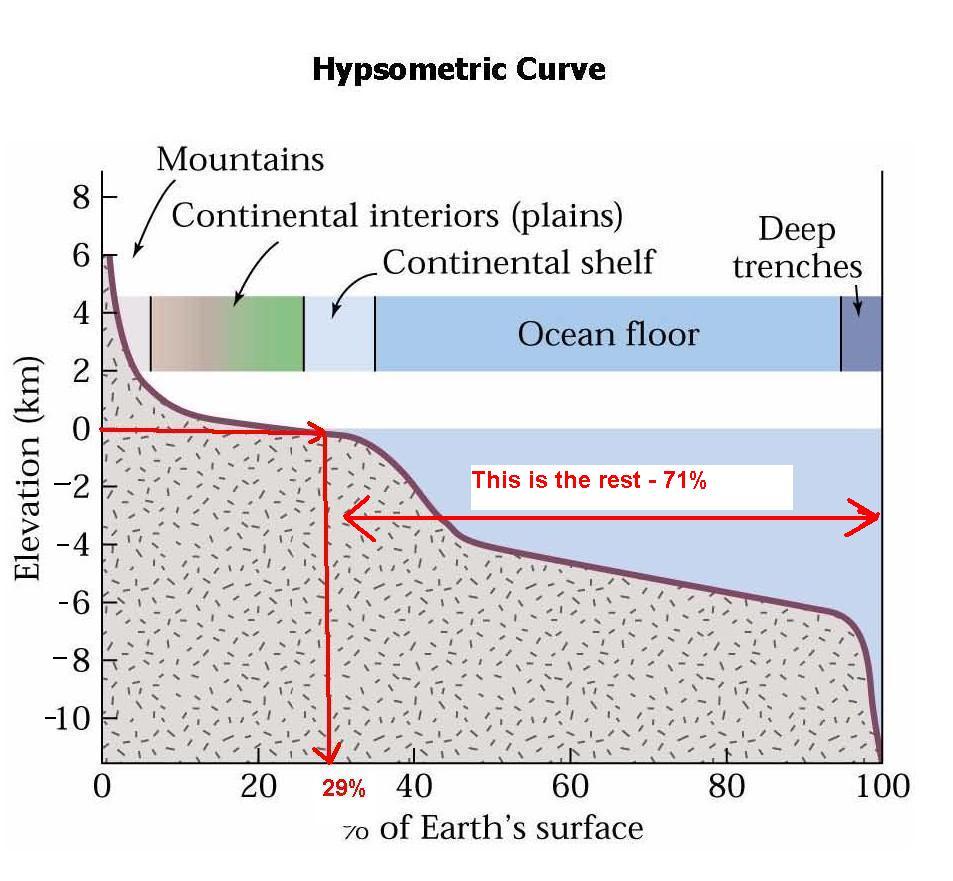
How To Read A Sea Level Curve Geological Digressions
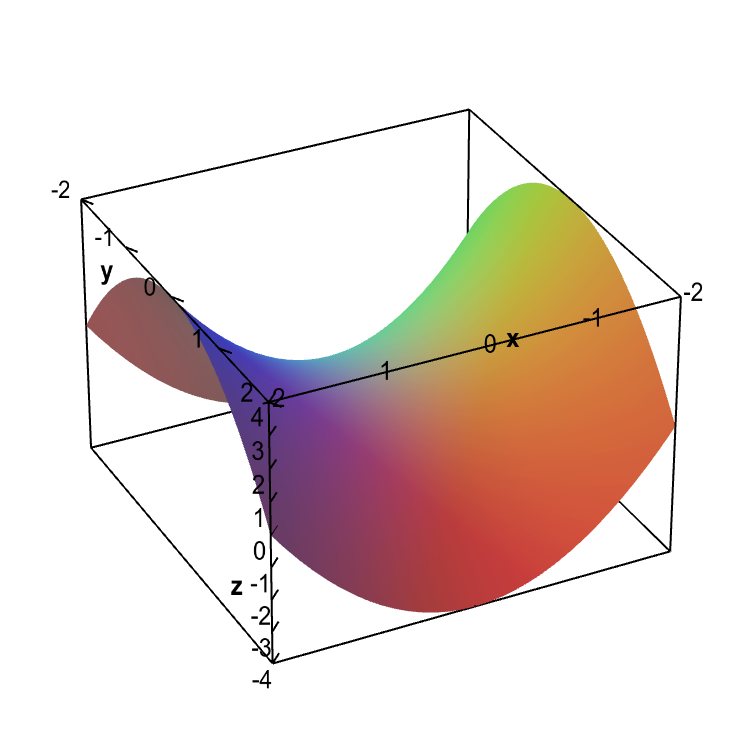


Level Set Examples Math Insight



Level Sets Math Insight



14 1 Functions Of Several Variables Mathematics Libretexts



Level Curves Examples



Slope Of A Level Curve Youtube
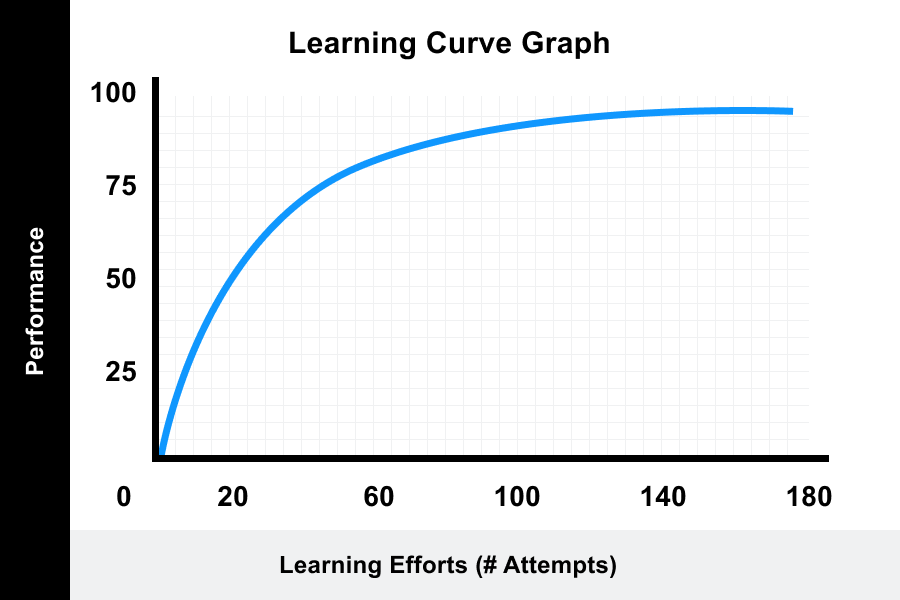


Learning Curve Theory Meaning Formulas Graphs
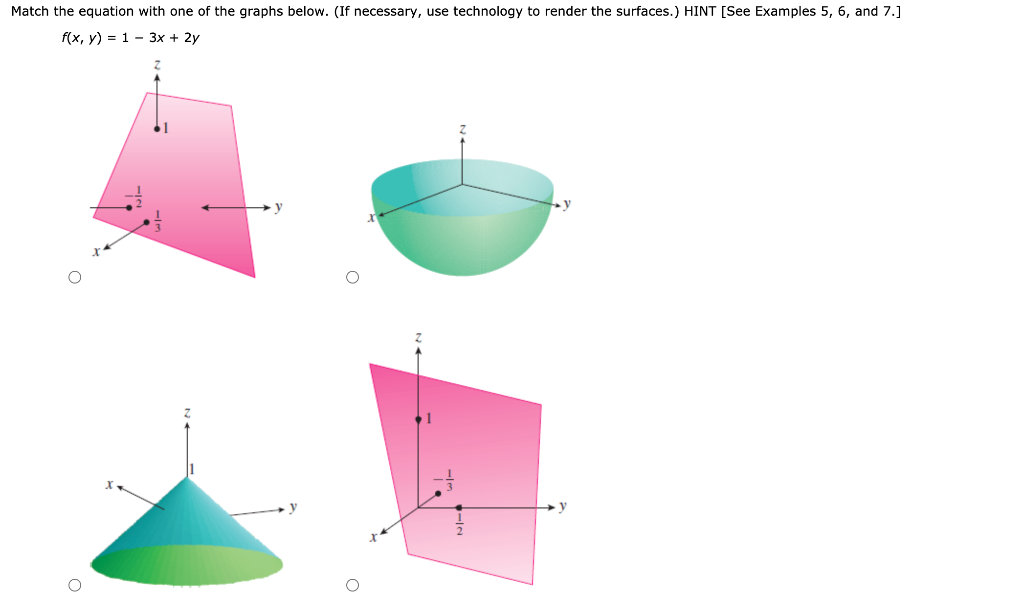


Refer To The Following Plot Of Some Level Curves O Chegg Com



Level Curves Examples Done In Mathematica Last Modified Spring 14


Other Instances Of Level Curves


Functions Of Several Variables Ximera


Elementary Calculus Example 5 Same Of Hyperbolic Paraboloid


Level Curves And Contour Plots



Introduction To Functions Of Several Variables



Applicable Mathematics 2 Examples 1 Level Curves



Applicable Mathematics 2 Examples 1 Level Curves



Level Curves



Introduction To Functions Of Several Variables


Level Curves And Contour Plots Mathonline



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Contour Plot An Overview Sciencedirect Topics
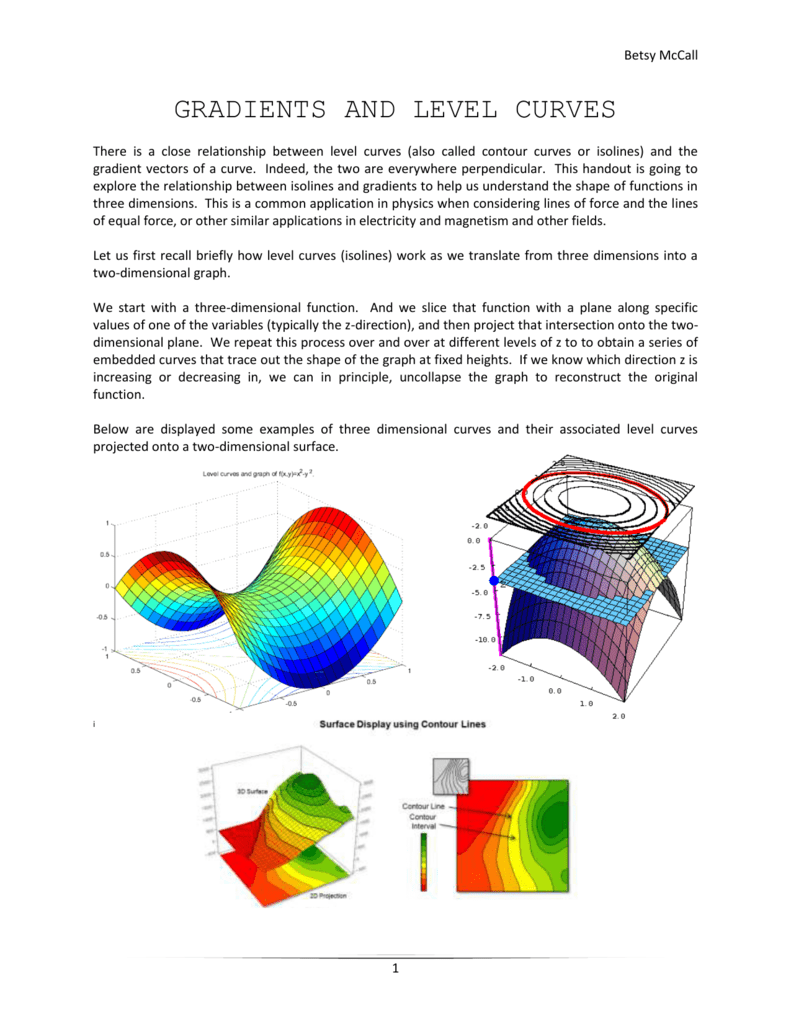


Gradients Level Curves


Examples Wednesday Feb 19



Level Curves Examples



Calculus Iii Functions Of Several Variables



Level Curves



Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram



Calculus Iii Functions Of Several Variables


12 1 Introduction To Multivariable Functions Mathematics Libretexts
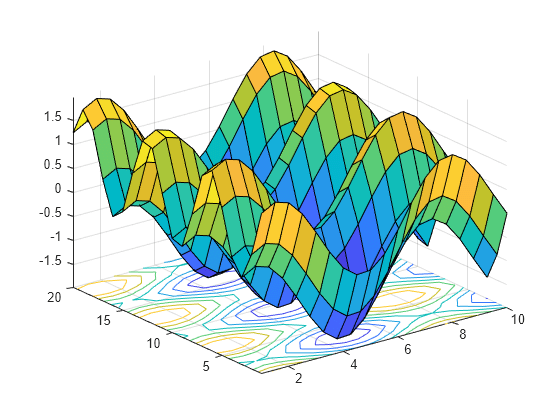


Contour Plot Under Surface Plot Matlab Surfc



Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram


Level Curves And Contour Plots Mathonline



Level Sets Math Insight


Level Sets Math Insight



Two Examples Of Eustatic Sea Level Curves That Show Significant Download Scientific Diagram



Level Set Wikipedia



L7 Evaluation Of Functions Domain And Range Level Curves And Surfaces Ppt Level Curves And Level Surfaces Math23 Multivariable Calculus General Course Hero



Level Curves Of Functions Of Two Variables Youtube


Level Set Examples Math Insight



Matb41h3 Midterm Detailed Examples For Drawing Level Curves Oneclass



Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram



Fun Math Art Pictures Benice Equation Scilab Example Plotting Implicit Curves Level Curves


Math 225 Calculus Iii



How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube



Introduction To Functions Of Several Variables



Calculus Iii Functions Of Several Variables



Graphs And Level Curves



Level Set Wikipedia



Level Set Wikipedia



Solved 3 Points Writing Prompt Typed 100 0 Words I Chegg Com
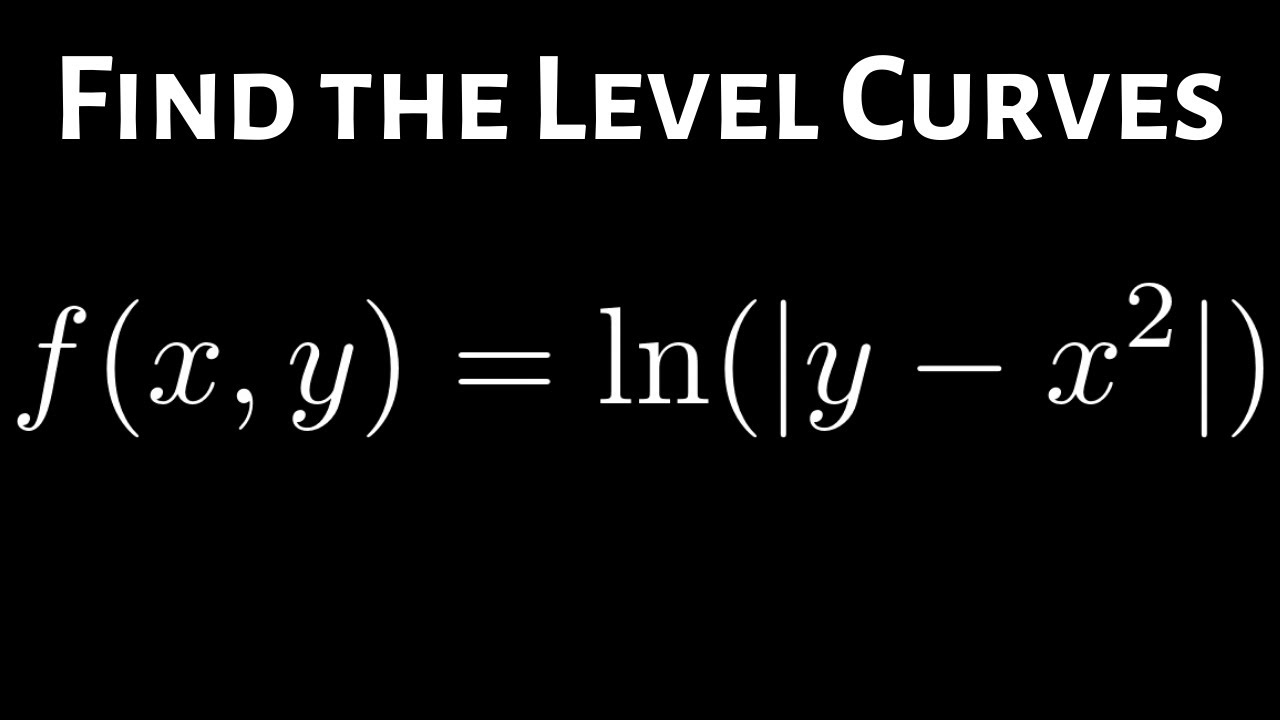


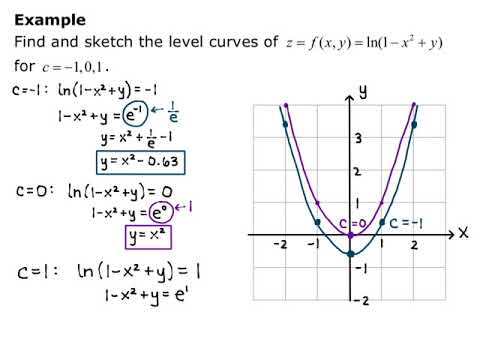
How To Find The Level Curves Of F X Y Ln Y X 2 Youtube



Level Sets Math Insight
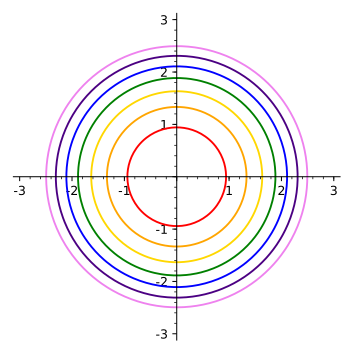


14 1 Functions Of Several Variables



Level Curves Calculus
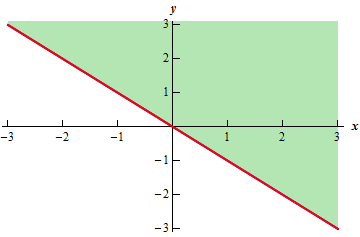


Calculus Iii Functions Of Several Variables



14 1 Functions Of Several Variables Mathematics Libretexts



Level Set Examples Math Insight



Calculus Iii Functions Of Several Variables


The Gradient And Directional Derivative


Level Curves And Contour Plots Mathonline


12 1 Introduction To Multivariable Functions Mathematics Libretexts


Level Curves And Contour Plots Mathonline
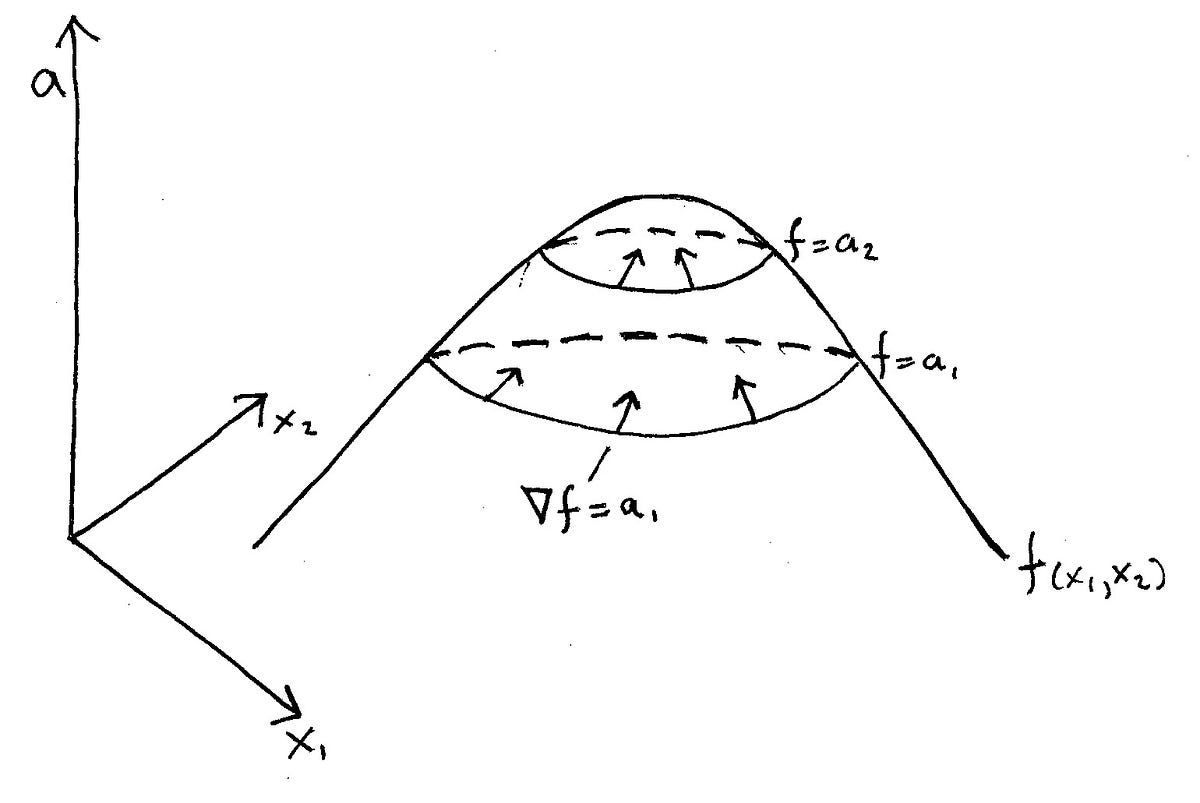


A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium
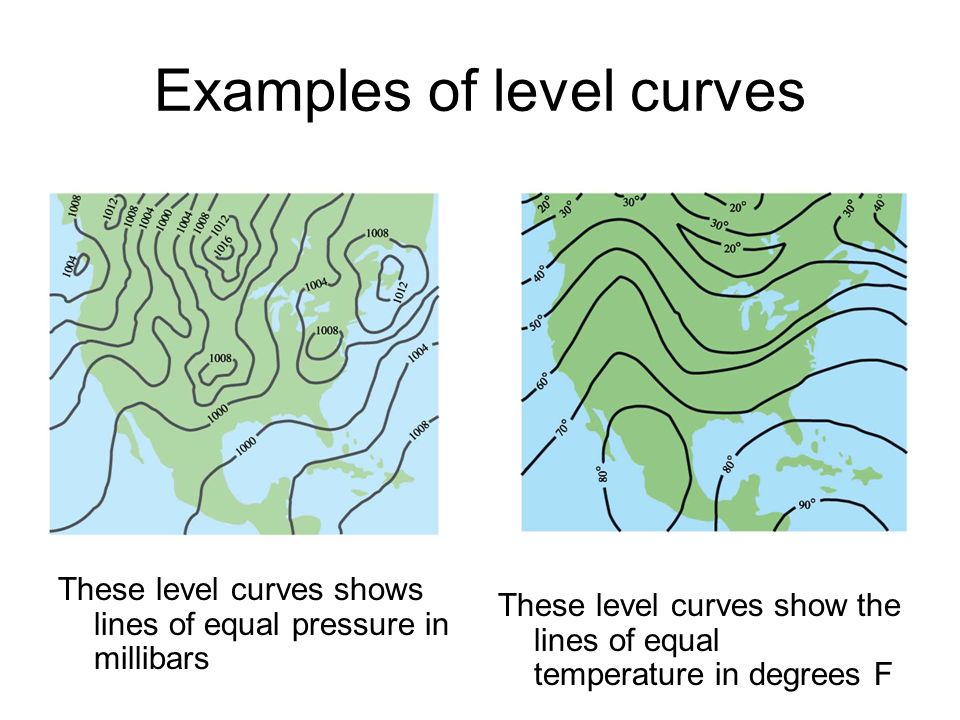


13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned



Solved Sketch The Level Curves For F X Y 2x 2 4y 2 Chegg Com



Level Curves Examples
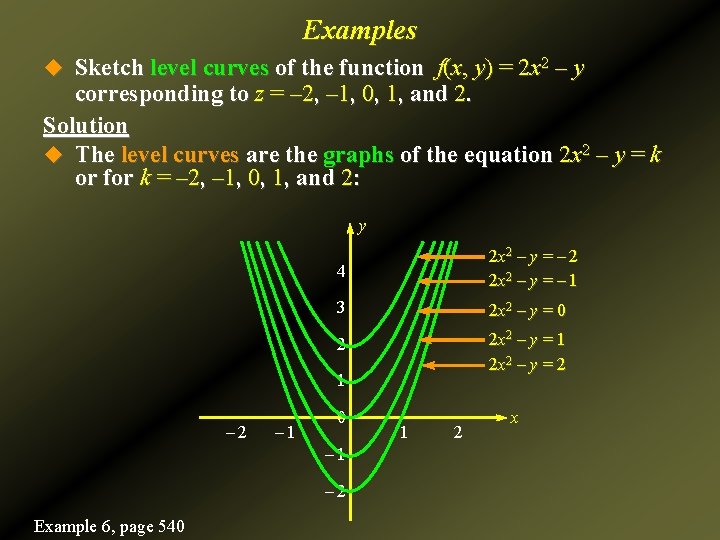


8 Calculus Of Several Variables U Functions Of


Math 225 Calculus Iii


